In everyday life, math seems straightforward: when you add two numbers together, the result is what you’d expect. But every now and then, a puzzle comes along that challenges the way we think. One such puzzle is: “When I take 5 and add 6, I get 11, but when I take 6 and add 7, I get 1. What am I?”
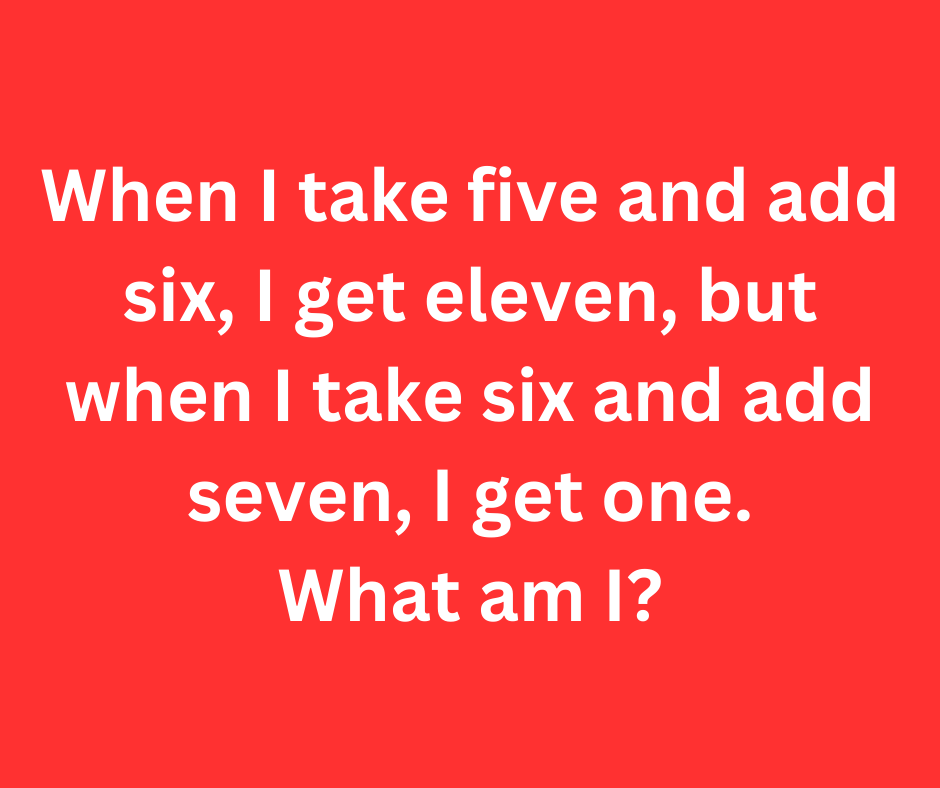
This intriguing riddle stirs up curiosity and makes you question traditional logic. The answer to this puzzle lies in the unique operations of a clock. Let’s dive in and uncover the solution, while also exploring why clock arithmetic is so captivating.
The Key to the Puzzle: A Clock’s Cyclic Nature
At first glance, this puzzle may seem like it’s breaking the rules of math. But the trick lies in understanding the cyclic nature of a clock. Clocks don’t work in a linear manner like regular numbers; instead, they operate in cycles of 12 hours.
When you add numbers on a clock, you’re not just moving forward; you’re rotating around the face of the clock. Once you hit 12, the count resets back to 1. This is why adding 6 to 7 doesn’t give you 13, but rather brings you back to 1. This process is known as modular arithmetic, specifically, modulo 12 when referring to clocks.
Exploring the First Step: 5 + 6 = 11
Let’s break down the first part of the puzzle: “When I take 5 and add 6, I get 11.” This is pretty straightforward because adding 6 to 5 on a clock simply moves the hand to 11.
Imagine starting at 5 o’clock and moving forward 6 hours. You pass through 6, 7, 8, 9, 10, and end up at 11. It’s just like normal addition, and there’s nothing tricky here. But things get more interesting with the next step.
Unraveling the Mystery: 6 + 7 = 1
Here’s where the puzzle gets fascinating. “When I take 6 and add 7, I get 1.” Wait, what? How can that be?
This happens because, on a clock, numbers loop around after 12. Once you hit 12, you don’t keep going to 13, 14, and so on. Instead, the clock wraps back to 1. So when you add 7 to 6, you’re essentially going past 12 and wrapping back to the beginning of the clock.
Start at 6 o’clock and count forward 7 hours:
- 6 + 1 = 7
- 6 + 2 = 8
- 6 + 3 = 9
- 6 + 4 = 10
- 6 + 5 = 11
- 6 + 6 = 12
- 6 + 7 = 1
This is why adding 7 to 6 on a clock lands you at 1 instead of 13. It’s all thanks to the circular nature of a clock.
What Is Modular Arithmetic?
The underlying principle here is modular arithmetic. This type of arithmetic involves numbers wrapping around after reaching a certain value, called the modulus. On a 12-hour clock, the modulus is 12, which means that when you reach 12, you start over at 1.
This kind of arithmetic is used in many everyday situations, not just clocks. Think about how days of the week work: after 7 days, you cycle back to the beginning of the week. It’s the same concept!
The Importance of Clock Puzzles
Clock puzzles, like this one, do more than just entertain us. They sharpen our problem-solving skills by forcing us to think outside the box. We’re so used to linear thinking—where 7 + 6 equals 13—that we often forget there are other ways numbers can behave.
Understanding clock arithmetic also gives us a deeper appreciation for how time works. It reminds us that not all systems are infinite; some things in life, like time, are cyclical. This is a valuable lesson that can be applied to many areas of life.
Unlocking the Secrets of Time: A Conclusion
So, what’s the takeaway from this intriguing puzzle? It’s that sometimes, the rules we’re used to don’t apply. In the world of clock arithmetic, numbers wrap around, and the familiar becomes unfamiliar. By understanding this, we not only solve the puzzle but also gain a new perspective on how time and numbers interact.
Next time you look at a clock, remember that it’s not just a simple tool for telling time. It’s also a source of captivating puzzles and a reminder that the world around us often works in cycles. Whether it’s hours on a clock, days of the week, or the changing of the seasons, life is full of these circular patterns. And sometimes, the best way to solve a problem is to break free from linear thinking and embrace the cycle.
So, what am I? I’m a clock—an ever-turning, ever-ticking reminder that sometimes, the answer to a puzzle isn’t in the numbers themselves, but in how those numbers behave.




